PLAN DE ALIMENTACION

DESARROLLO DE TRONCO DE CONO DE REVOLUCION

En el desarrollo plano vemos que tiene dos bases circulares. La altura es la distancia entre las bases, y la generatriz es el segmento que lo ha generado.

El área del tronco de cono será la suma del área lateral y del área de los círculos de las dos bases

DESARROLLO DE CONO DE REVOLUCION

En el desarrollo de un cono recto se aprecia que su lateral es un sector circular de radio g. ¿Qué porción de círculo tiene ese sector? ¿Te animas a averiguarlo?

• La circunferencia completa tiene una longitud de 2πr.
• El sector circular tiene una longitud de 2πr.
• El área de la base es πr².

DESARROLLO DE TRONCO DE cilindro recto O Cilindro truncado

Cilindro truncado

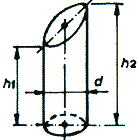
DESARROLLO DE UN CILINDRO RECTO

Construir el desarrollo de un cilindro recto

Queremos construir el desarrollo del cilindro recto mostrado en la figura 1.

Las dos bases del cilindro son círculos, cada uno con un radio de 1,5 cm. El desarrollo de su “cara” lateral es un rectángulo. La altura de este rectángulo es la misma que la del cilindro (3 cm), y su base mide lo mismo que el perímetro de la circunferencia de la base del cilindro.
Para calcular este perímetro, usaremos la fórmula P = 2 ×  × r, donde P, y r son respectivamente el perímetro, el número pi (aproximadamente 3,14) y la longitud del radio.
Tenemos que P = 2 × 3,14 × 1,5 = 9,42. Por lo tanto, el perímetro de la circunferencia (la base del rectángulo) mide aproximadamente 9,4 cm.
Las figuras 2 y 3 muestran el desarrollo del cilindro y cómo doblarlo.


Nota: un cilindro recto puede tener varios desarrollos. La figura 4 muestra otro posible desarrollo para el cilindro de la figura 2.

CONO DE REVOLUCION

                                                             CONO DE REVOLUCION
En geometría, un cono recto es un sólido de revolución generado por el giro de un triángulo rectángulo alrededor de uno de sus catetos. Al círculo conformado por el otro cateto se denomina base y al punto donde confluyen las generatrices se llama vértice.
Superficie cónica se denomina a toda superficie reglada conformada por el conjunto de rectas que teniendo un punto común (el vértice), intersecan a una circunferencia no coplanaria.

Desarrollo del cono

Elementos del cono

Eje

Es el cateto fijo alrededor del cual gira el triángulo.

Base

Es el círculo que forma el otro cateto.

Altura

Es la distancia del vértice a la base.

Generatriz

Es la hipotenusa del triángulo rectángulo.

Por el teorema de Pitágoras la generatriz del cono será igual a:

Área lateral de un cono

Área de un cono

Volumen de un cono

Ejemplos

Para una fiesta, Luís ha hecho 10 gorros de forma cónica con cartón. ¿Cuánto cartón habrá utilizado si las dimensiones del gorro son 15 cm de radio y 25 cm de generatriz?

Calcula el área lateral, total y el volumen de un cono cuya generatriz mide 13 cm y el radio de la base es de 5 cm.

Calcula el área lateral, total y el volumen de un cono cuya altura mide 4 cm y el radio de la base es de 3 cm.

ACTIVIDAD

Resolver los ejercicios de la actividad nº 19 del texto del ministerio de educación pag. 130.